En matemáticas, un número irracional es un número que no puede ser expresado como una fracción 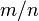 , donde
, donde  y
y  son enteros y
son enteros y  es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
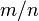 , donde
, donde  y
y  son enteros y
son enteros y  es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
no puede representar un número racional. A tales números se los nombra «números irracionales». Esta denominación significa la imposibilidad de representar dicho número como razón de dos números enteros.
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclídeas.


Esta publicación ha sido mi primera practica del diplomado de las Tics.
ResponderEliminar